Cumulative Interest Payment

When it comes to understanding the full cost of a loan, knowing just the monthly payment isn’t enough as the interest paid over time can be significant. That’s where Excel’s powerful CUMIPMT function comes into play. In this post, we’ll walk step-by-step through how to calculate cumulative interest over a given loan period and explore how much money can be saved with an early payoff. Let’s simplify complex financial forecasting right from within Excel.

Video

What is the CUMIPMT Function?

The CUMIPMT function in Excel is a financial function that calculates the cumulative interest paid on a loan between two specified periods. This function is especially useful for long-term financial planning and evaluating the impact of different payment strategies.

Function Syntax:

=CUMIPMT(rate, nper, pv, start_period, end_period, type)

• rate: Interest rate per period (monthly, if applied monthly)
• nper: Total number of payment periods
• pv: Present value or loan amount
• start_period: Start period for interest calculation
• end_period: End period up to which interest is calculated
• type: Timing of payments (0 = end of period, 1 = beginning)

Step-by-Step Walkthrough

We’ll now look at three hands-on examples to make sense of how to use CUMIPMT for real-world loan analysis, including how to estimate interest savings from an early loan payoff.

Exercise 1: Calculating Interest Paid in a Specific Month

Suppose we’ve taken out a $100,000 loan at a 5% annual interest rate, repaid over 30 years (or 360 months).

Inputs:

• Interest Rate: 5% in cell C5
• Number of Months: 360 in cell C6
• Loan Amount: 100,000 in cell C7
• Desired end month: 1 (cell C10)

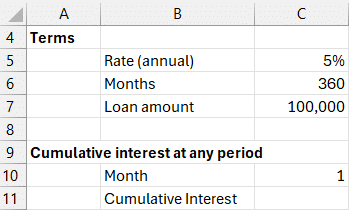
Formula in C11:

=-CUMIPMT(C5/12, C6, C7, 1, C10, 0)

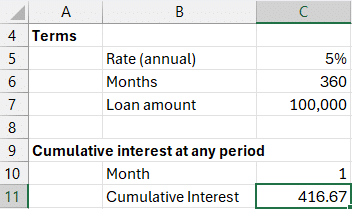
The result is: $416.67, which represents the interest portion of the first payment.

Want to view cumulative interest over two months? Simply change C10 to 2, and Excel updates the total interest paid to that point.

Exercise 2: Total Interest Over the Loan’s Life

With the same loan data, let’s calculate the total interest paid over 30 years.

Formula in C10:

=-CUMIPMT(C5/12, C6, C7, 1, C6, 0)

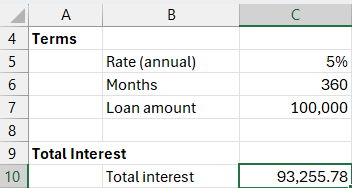
This shows a staggering total interest of $93,255.78. On a $100,000 loan, we end up paying nearly the same amount in interest as we borrowed. That’s the real cost of borrowing over time. Can we reduce the amount of interest paid, even if we have an existing loan with these terms? Let’s head to the next exercise.

Exercise 3: Calculate Interest Savings from Early Payoff

Here’s where things get interesting. What if we pay off our loan early … say, halfway through the full term?

Additional Input:

• Early payoff month: 180 (15 years) in C10

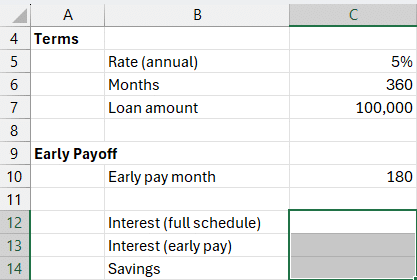
Step 1: Interest for full loan term in C12

=-CUMIPMT(C5/12, C6, C7, 1, C6, 0)

Step 2: Interest paid until early payoff in C13

=-CUMIPMT(C5/12, C6, C7, 1, C10, 0)

Step 3: Interest savings in C14

= C12-C13

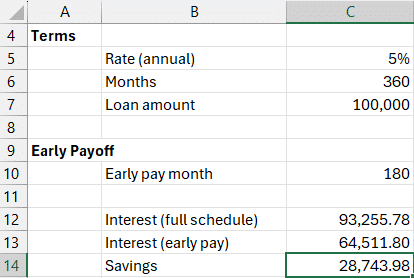
We find that by paying off the loan at month 180, we save $28,743 in interest.

Now that our formulas are entered, we can change the assumption values as desired!

Summary: Why Use CUMIPMT?

• It provides clear insight into interest costs over time
• Helps in visualizing benefits of extra or early payments
• Works well with variable inputs for scenario planning
• A great tool for financial literacy and decision-making

Download This Excel File

Want to try this out yourself? Simply open it and experiment with your own loan terms.

Frequently Asked Questions

1. What does CUMIPMT mean?

It stands for “Cumulative Interest Payment” and calculates how much interest has been paid between any two periods on a loan.

2. Why is the result negative?

Financial functions in Excel use a cash flow convention where money going out (payments) is negative. You can reverse the sign with a leading minus sign in front of the formula.

3. What does the “type” argument do?

It determines when payments occur: 0 for end of period (most common), 1 for beginning of period.

4. Can it calculate total principal paid?

No, CUMIPMT only calculates interest. Use CUMPRINC for cumulative principal payments.

5. Does this consider extra payments?

No, CUMIPMT assumes regular scheduled payments. For modeling extra payments, consider using Excel’s amortization schedules manually.

6. Why divide rate by 12?

Most loans are monthly, so we convert the annual rate to a monthly rate by dividing by 12.

7. Can I use this for credit card interest?

You can, but be cautious as credit card interest often compounds differently and may vary month to month.

8. Can I automate early payoff calculations?

Yes! With cell references and structured inputs, you can model many early payoff scenarios dynamically.